КОЛО, ВПИСАНЕ В ЧОТИРИКУТНИК
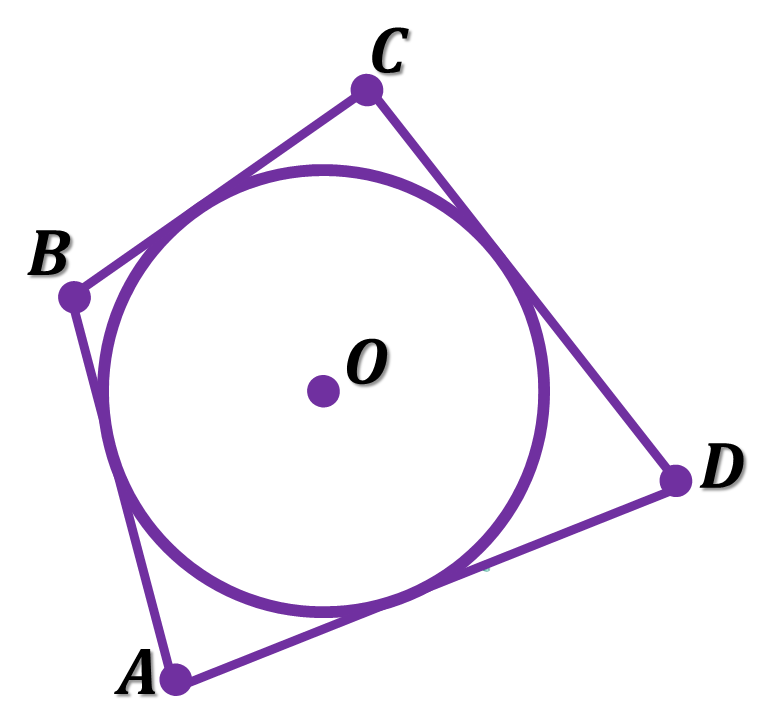
Коло, що дотикається до всіх сторін чотирикутника, називається вписаним у цей чотирикутник. При цьому чотирикутник називають описаним навколо кола.
Центром вписаного кола є точка перетину бісектрис кутів чотирикутника, оскільки ця точка O – рівновіддалена від усіх сторін чотирикутника.
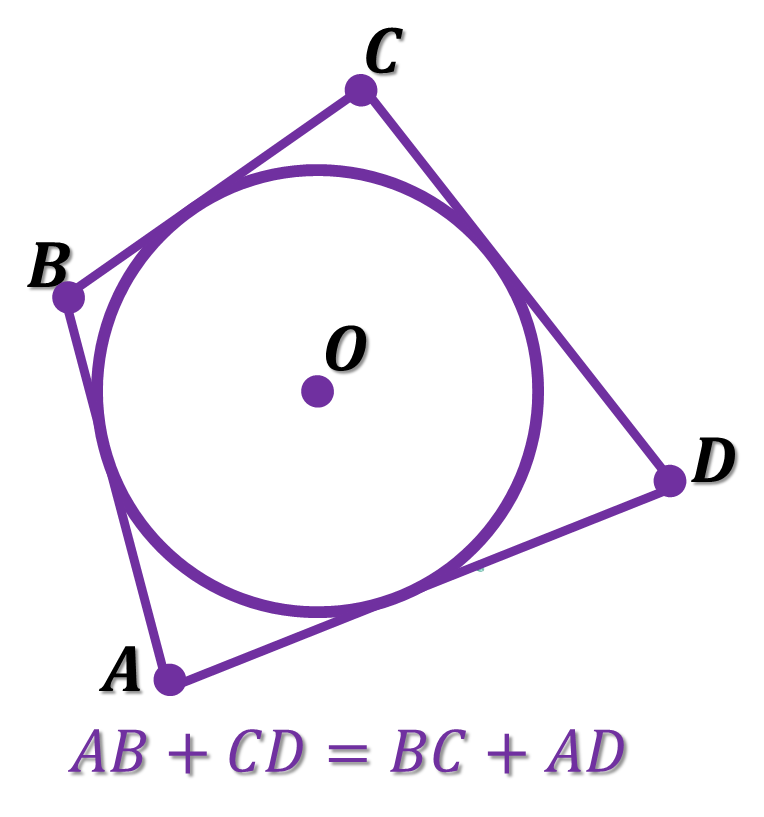
Якщо чотирикутник є описаним навколо кола, то суми його протилежних сторін рівні.
Якщо в опуклому чотирикутнику суми протилежних сторін рівні, то цей чотирикутник є описаним.
КОЛО, ВПИСАНЕ У КВАДРАТ

Оскільки діагоналі квадрата є бісектрисами його кутів, то центр вписаного кола збігається з точкою перетину діагоналей квадрата.
Діаметр кола дорівнює стороні квадрата. Нехай сторона квадрата дорівнює a, а радіус вписаного кола – r.
КОЛО, ВПИСАНЕ У РОМБ

Оскільки діагоналі ромба є бісектрисами його кутів, то центр вписаного кола збігається з точкою перетину діагоналей ромба.
Діаметр кола дорівнює будь-якій висоті ромба, оскільки у ромба всі висоти рівні. Нехай висота ромба дорівнює h, а радіус вписаного кола – r.
У будь-який ромб можна вписати коло.
Якщо в паралелограм вписати коло, то він є ромбом.
Центр вписаного кола є точкою перетину діагоналей ромба.
КОЛО, ВПИСАНЕ У ТРАПЕЦІЮ
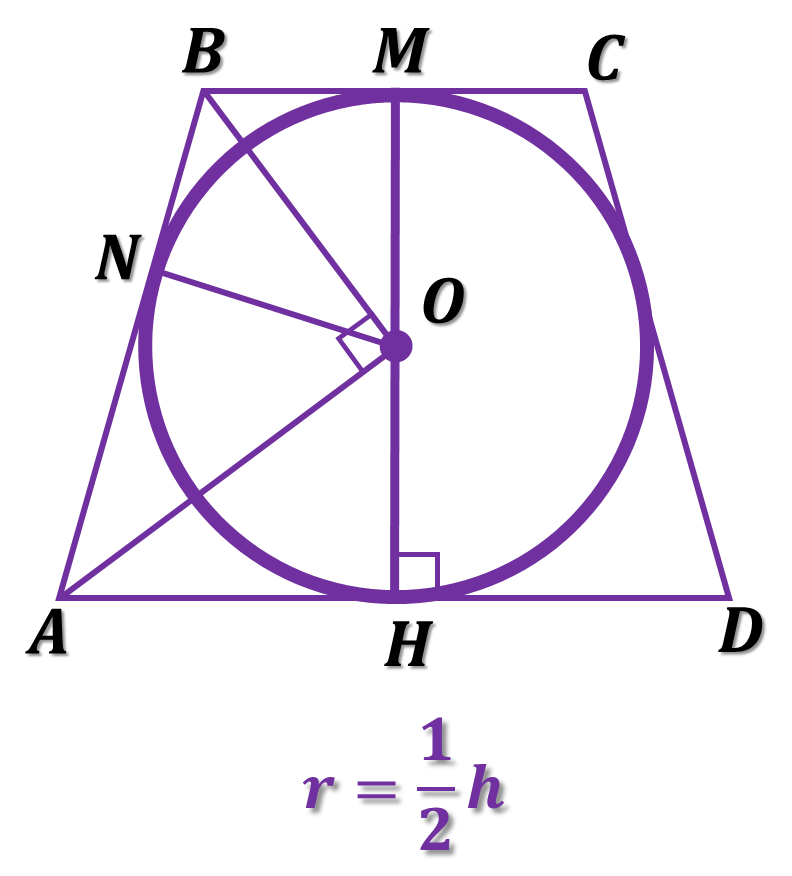
Коло можна вписати у кожну з трьох видів трапеції, для яких суми протилежних сторін рівні.
Оскільки MH = h – висота трапеції і діаметр кола, то r=1/2 h, де r – радіус вписаного кола.
У рівнобічній трапеції, в яку можна вписати коло, бічна сторона дорівнює середній лінії трапеції.

КОЛО, ОПИСАНЕ НАВКОЛО ЧОТИРИКУТНИКА

Коло називається описаним навколо чотирикутника, якщо всі вершини чотирикутника лежать на колі. При цьому чотирикутник називають вписаним у коло.
Центром кола, описаного навколо чотирикутника, є точка перетину серединних перпендикулярів до його сторін, оскільки точка перетину серединних перпендикулярів рівновіддалена від вершин чотирикутника.
Якщо чотирикутник є вписаним, то сума його протилежних кутів дорівнює 180°.
Якщо в чотирикутнику сума протилежних кутів дорівнює 180°, то він є вписаним.
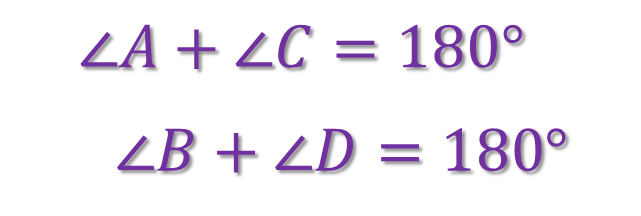
КОЛО, ОПИСАНЕ НАВКОЛО ПРЯМОКУТНИКА

Навколо будь-якого прямокутника можна описати коло
Якщо паралелограм вписаний у коло, то він є прямокутником
Центр описаного навколо чотирикутника кола, є точкою перетину серединних перпендикулярів, проведених до його сторін.
Центр описаного навколо прямокутника кола збігається з точкою перетину його діагоналей.
Центр кола, описаного навколо прямокутника збігається з точкою перетину його діагоналей
де R – радіус описаного кола, d = AC = BD – діагональ прямокутника.
КОЛО, ОПИСАНЕ НАВКОЛО КВАДРАТА

Центр кола, описаного навколо квадрата збігається з точкою перетину його діагоналей
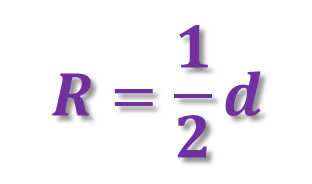
де R – радіус описаного кола, d = AC = BD – діагональ квадрата.
КОЛО, ОПИСАНЕ НАВКОЛО ТРАПЕЦІЇ
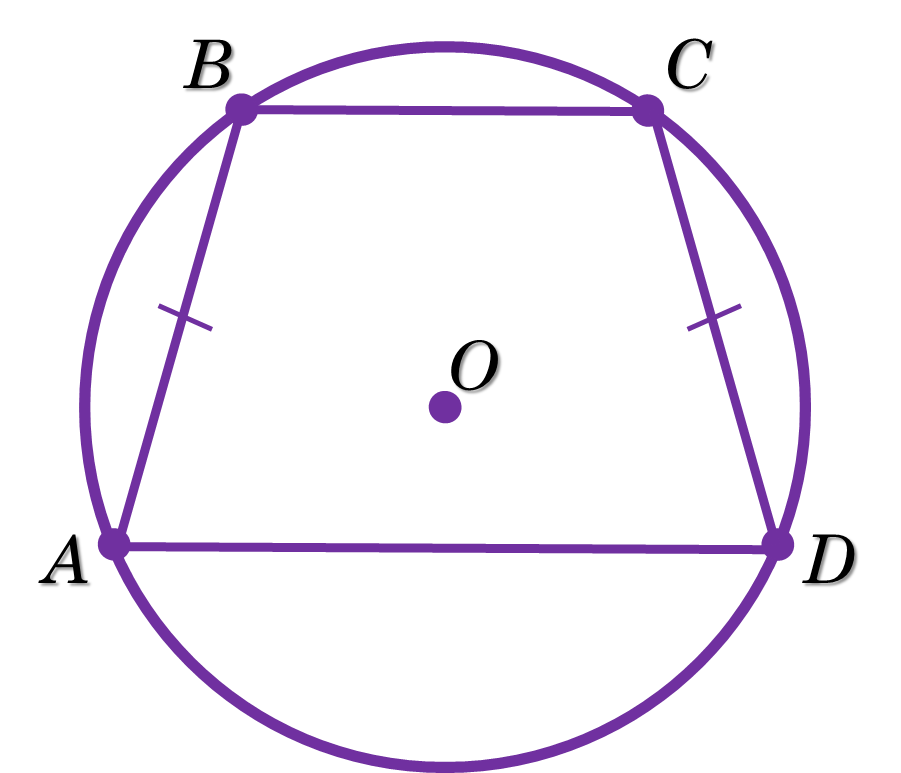
Навколо рівнобічної трапеції можна описати коло.
Якщо трапеція вписана в коло, то вона рівнобічна.
