Правило суми
Скількома способами можемо вибрати одну шоколадку або одне печиво?

Оскільки шоколадку можна вибрати 3-ма способами, а печиво 4-ма способами, то однин із них можна вибрати 3+4=7 способами.
Правило суми:
Якщо деякий елемент А можна вибрати m способами, а деякий елемент В – n способами (причому будь-який вибір елемента А відрізняється від вибору елемента В), то вибрати А або В можна m+ n способами.
Правило добутку
Скількома способами можемо вибрати одну шоколадку і одне печиво?

Оскільки можемо вибрати будь-яку одну з 3-х шоколадок то парою до неї може бути будь-яке одне з 4-х печив, тоді можемо вибрати одну шоколадку і одне печиво 3∙4=12 способами.
Правило добутку:
Якщо деякий елемент А можна вибрати m способами, а після кожного такого вибору інший елемент В можна вибрати k способами, то пару об’єктів А і В можна вибрати m • k способами.
Розділ математики, що вивчає способи розв’язування подібних задач називається комбінаторикою, а самі задачі – комбінаторними.
Вибрані (або вибрані й розміщені) групи елементів називаються сполуками. В шкільному курсі ми будемо розглядати сполуки без повторень.
Факторіал
Розглянемо задачу:
Скільки чотирицифрових чисел можна скласти із цифр 5, 6, 7, 8 причому так, щоб у кожному числі всі цифри були різними?
Розв’язання.
Першою цифрою в такому чотирицифровому числі може бути будь-яка із чотирьох цифр: 5, 6, 7 або 8. Маємо: 4 варіанти.
Оскільки всі цифри в цьому чотирицифровому числі мають бути різними, то якою б не була перша цифра, другою цифрою числа може бути будь-яка з тих трьох цифр, що залишилися. Отже, для кожного із чотирьох варіантів вибору першої цифри існує 3 варіанти вибору для другої цифри. Використовуючи правило добутку, маємо, шо перші 2 цифри чотирицифрового числа можна вибрати 4∙3=12 способами.
Міркуючи аналогічно, стверджуємо, що для кожного із цих 12 варіантів вибору перших двох цифр існує 2 варіанти вибору третьої цифри. Справді, якщо першими двома цифрами вибрано, наприклад, цифри 5 і 6, то третьою цифрою може бути будь-яка з двох цифр – 7 або 8. Використовуючи правило добутку, доходимо висновку, що перші 3 цифри можна вибрати 4∙3∙2=24 способами.
Оскільки всі цифри в чотирицифровому числі мають бути різними, то зрозуміло, що перші 3 цифри числа однозначно визначають останню четверту цифру. Тому із цифр 5, 6, 7, 8 можна скласти 4∙3∙2∙1=24 чотирицифрових числа так, щоб у кожному числі всі цифри були різними.
Відповідь. 24.
Кількість різних чотирицифрових чисел у яких жодна цифра не повторюється можна скласти 4∙3∙2∙1=24 способами.
Під час розв’язування прикладу нам довелося обчислювати добуток 4∙3∙2∙1. У комбінаторних задачах добуток послідовних натуральних чисел від 1 до n зустрічається настільки часто, що отримав спеціальну назву «”факторіал”» і позначення n! (запис «n!» читають «ен факторіал»): n!=1∙2∙3∙…∙n
Наприклад, 5!=1∙2∙3∙4∙5=120
За означенням 0!=1 і 1!=1
Приклад. Із міста A до міста B проходять 4 дороги, а з міста B до міста C проходять 3 дороги. Скількома способами можна проїхати з міста A до міста C?

Розв’язання.
Дорогу від міста A до міста B можна обрати 4-ма способами, а дорогу від міста B до міста C – 3-ма способами, то за правилом добутку дорогу від міста A до міста C можна подолати 4∙3=12 способами.
Відповідь: 12.
Приклад. На вершину гори прокладено 5 маршрутів. Скількома способами альпініст може піднятися на гору та спуститися з неї? Дайте відповідь на це запитання також за умови, коли підйом і спуск мають відбуватися за різними маршрутами.
Розв’язання.
Розглянемо перший випадок, коли альпініст може спускатися тим же маршрутом, що і піднявся. Так як в цьому випадку він може піднятися 5 маршрутами та спуститися 5 маршрутами, то способів підйому та спуску існує:
5∙5=25 способів
Розглянемо другий випадок, коли альпініст не може спускатися тим же маршрутом, що і піднявся. В цьому випадку альпініст може піднятися 5 способами і спуститися 4 способами, так як не може використовувати для спуску маршрут підйому. Отже способів підйому та спуску існує:
5∙4=20 способів
Відповідь: 25 способів у 1-му випадку і 20 способів у 2-му випадку.
Приклад. Скільки чотирицифрових чисел можна записати за допомогою цифр 1, 2, 3, 4, 5, 6, 7?
Розв’язання.
Так як цифри можуть повторюватися, то для вибору кожної цифри існує 7 способів, отже для запису числа існує:
7∙7∙7∙7=7^4=2401 способів
Відповідь: 2401 способів.
Приклад. На рисунку показано схему доріг, які ведуть з міста A до міста D. Скількома способами можна проїхати з міста A до міста D?
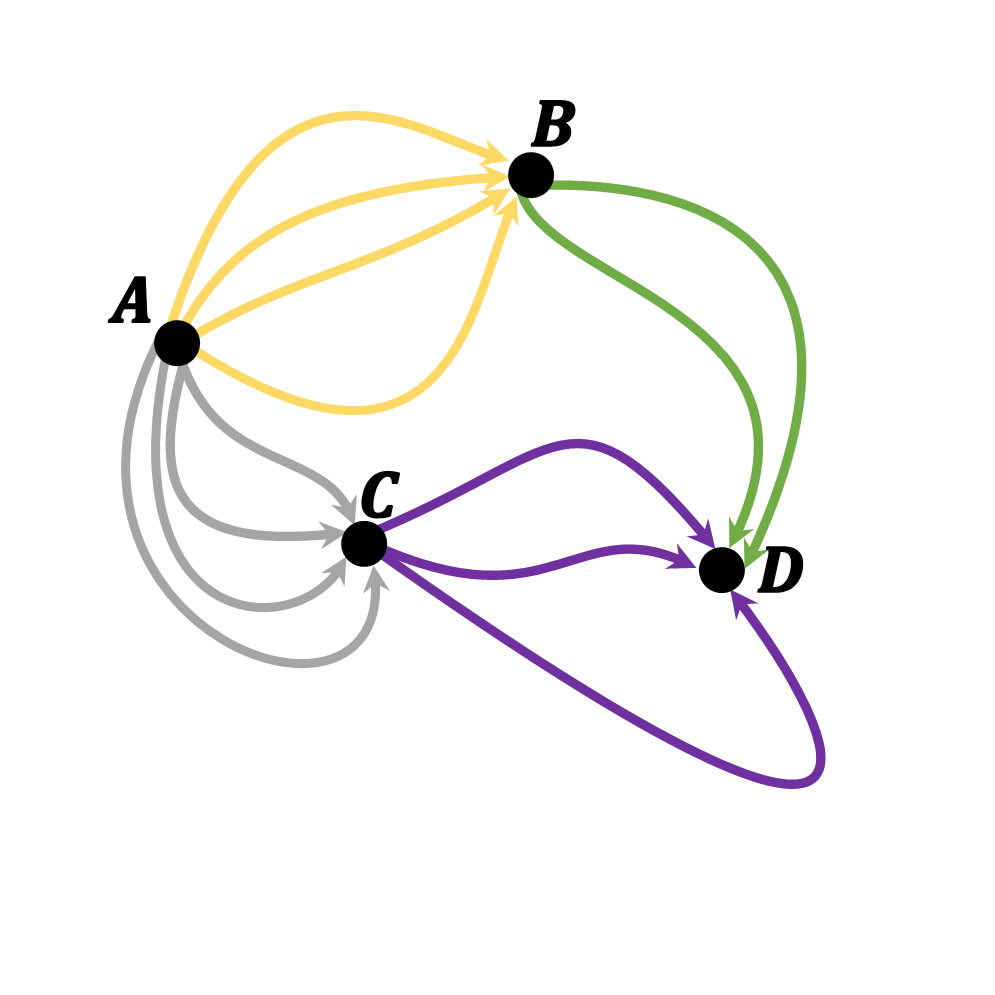
Розв’язання.
Так як з міста A до міста D через місто B можна проїхати 4∙2=8 способами, а через місто C 4∙3=12 способами, то загалом до з міста A до міста D можна проїхати 8+12=20 способами.
Відповідь: 20.
Приклад. Скільки існує трицифрових чисел, усі цифри яких парні?
Розв’язання.
Існує 5 парних цифр: 0, 2, 4, 6, 8
Скількома способами можемо обрати першу цифру для нашого трицифрового числа?
(Маємо 4 способи, так як не можемо поставити нуль як першу цифру числа)
Так як на перше місце трицифрового числа можемо поставити одну з 4-х цифр і на кожне наступне одну з 5 цифр, то можемо отримати: 4∙5∙5=100 чисел.
Відповідь: 100.
Приклад. Монету кидають 4 рази. Скільки різних послідовностей гербів і цифр можна отримати?
Розв’язання.
При кожному підкиданні монети завжди будуть можливі 2 випадки (герба або цифра), отже за 4 підкидання можливі 2∙2∙2∙2=2^4=16 випадків
Відповідь:16.
Приклад. Скільки трицифрових парних чисел можна записати за допомогою цифр 0,1,2,3,4,5,6?
Розв’язання.
Так як першу цифру можемо вибрати 6 способами (нуль не може бути першою цифрою), другу цифру можемо вибрати 7 способами а третю цифру 4 способами (так як число за умовою має бути парним) ⇒ кількість чисел можна записати 6∙7∙4=168 способами.
Відповідь: 168.
Приклад. Скільки існує п’ятицифрових чисел, які діляться націло на 5?
Розв’язання.
Маємо 10 цифр: 0,1,2,3,4,5,6,7,8,9.
Нуль не може бути першою цифрою, тому для вибору першої цифри маємо 9 способів.
Другу, третю та четверту цифру до п’ятицифрового числа можемо обрати 10∙10∙10=10^3
П’ятицифрове число за умовою має ділитися націло на 5, тому для вибору останньої цифри існує 2 способи: 0 або 5
Отже, існує 9∙10^3∙2=18000 п’ятицифрових чисел, які діляться націло на 5
Відповідь: 18000.