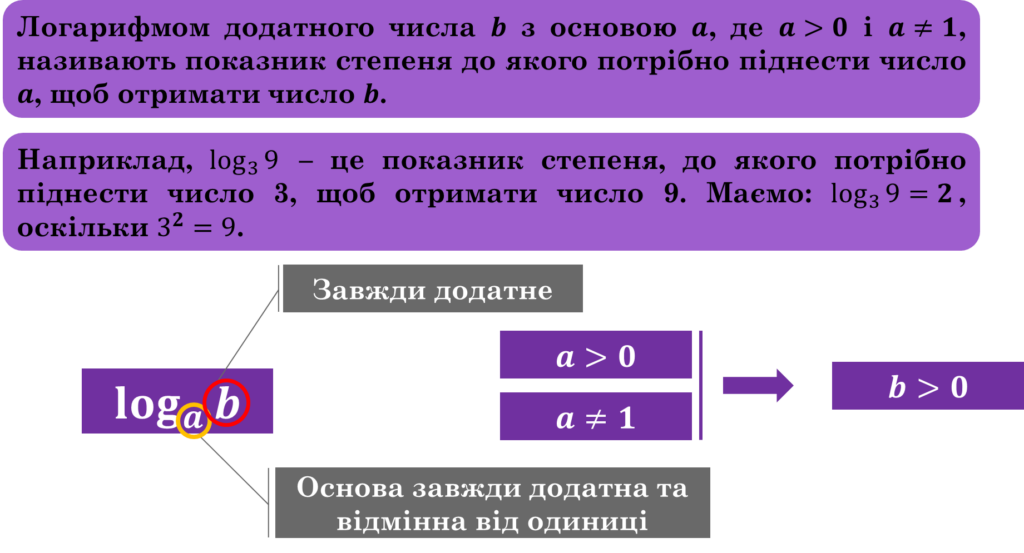
Логарифмом додатного числа b з основою a, де a>0 і a≠1, називають показник степеня до якого потрібно піднести число a, щоб отримати число b.
Наприклад, log39 – це показник степеня, до якого потрібно піднести число 3, щоб отримати число 9. Маємо: log3 9=2, оскільки 32=9.


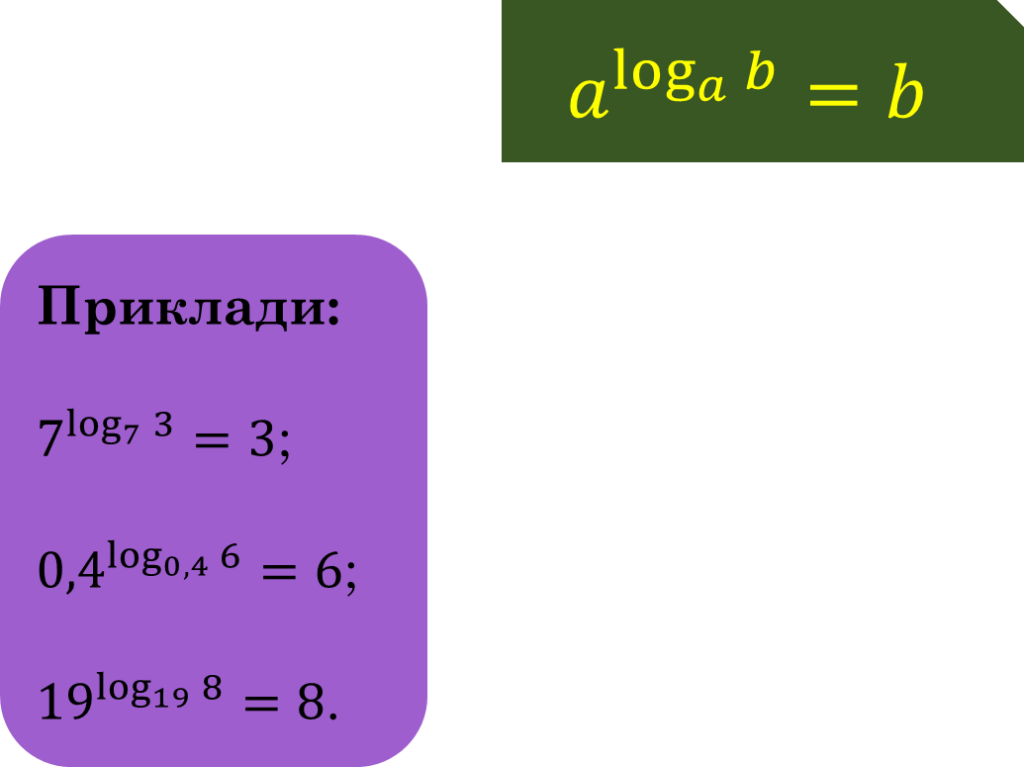
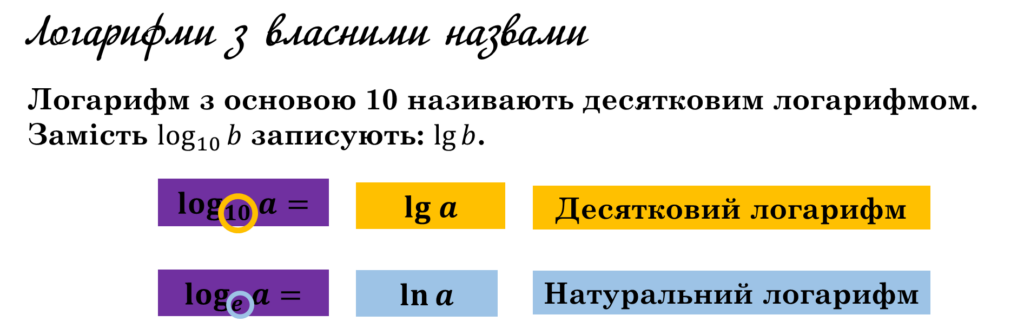
Логарифм від’ємного числа і нуля не існує.
Операцію знаходження логарифма числа називають логарифмуванням
Логарифм одиниці за будь-якою основою дорівнює нулю
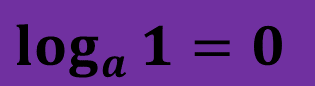
Логарифм числа, яке збігається з основою, дорівнює одиниці
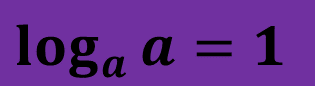
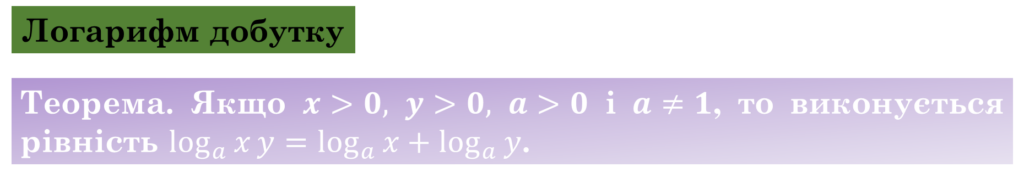
Логарифм добутку додатних чисел дорівнює сумі логарифмів множників.
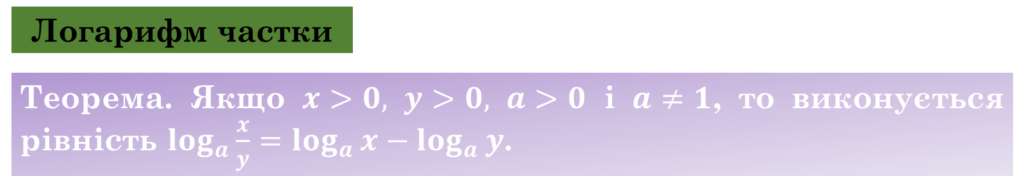
Логарифм частки додатних чисел дорівнює різниці логарифмів діленого і дільника.
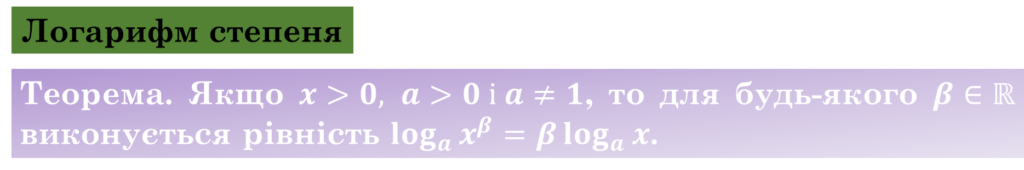
Логарифм степеня додатного числа дорівнює добутку показника степеня на логарифм основи цього степеня.

Логарифм додатного числа b за старою основою a дорівнює логарифму цього самого числа b за новою основою c, поділеному на логарифм старої основи a за новою основою c.
