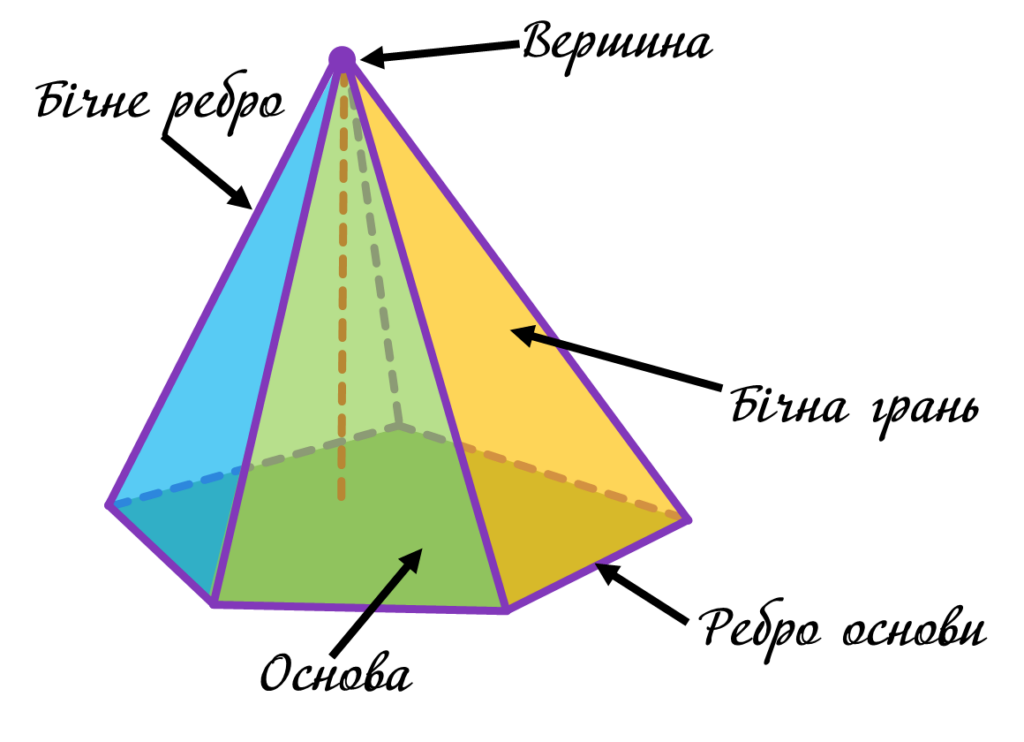
Піраміда – це многогранник, у якого одна з граней, яку називають основою, є довільним многокутником, а інші грані – трикутники зі спільною вершиною.
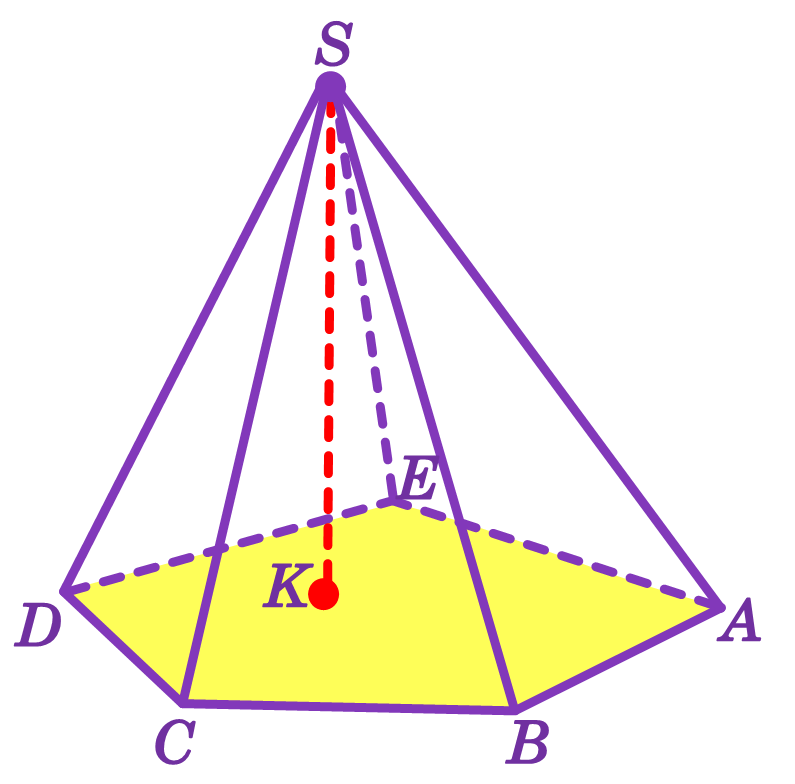
На рисунку зображено піраміду, основа якої – многокутник ABCDE, інші грані – трикутники ABS, BCS, CDS, DES, AES. Ці грані називають бічними гранями піраміди. Їхню спільну точку – точку S – називають вершиною піраміди. Піраміду, зображену на рисунку, називають пірамідою SABCDE. Ребра піраміди, які сполучають вершину піраміди з вершинами основи піраміди, називають бічними ребрами піраміди. На рисунку відрізки SA, SB, SC, SD і SE – бічні ребра піраміди.

Многогранник, одна грань якого – n-кутник, а решта граней – трикутники, що мають спільну вершину, називають n-кутною пірамідою.
На рисунку зображено п’ятикутну піраміду.
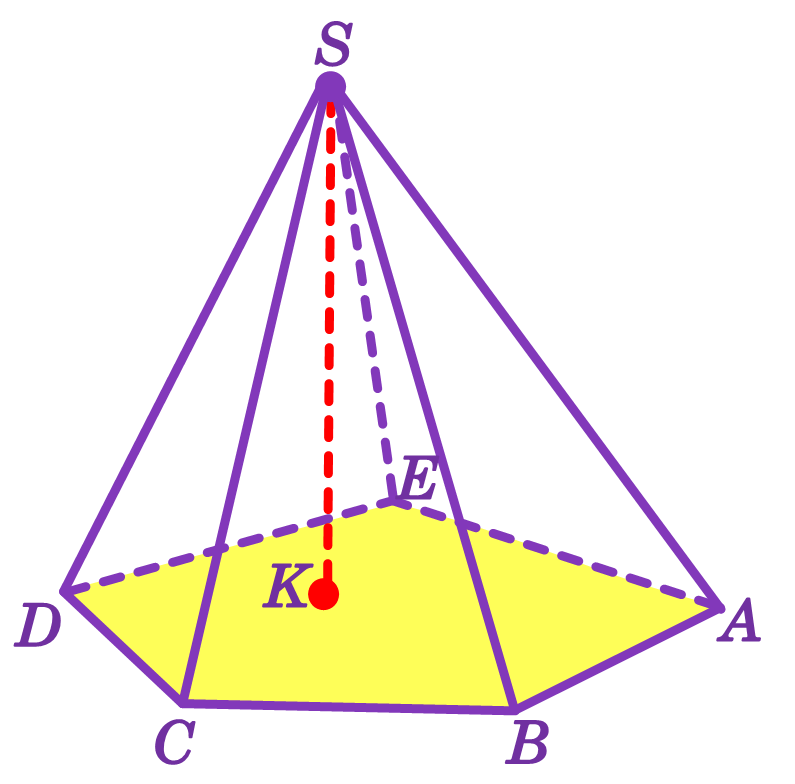
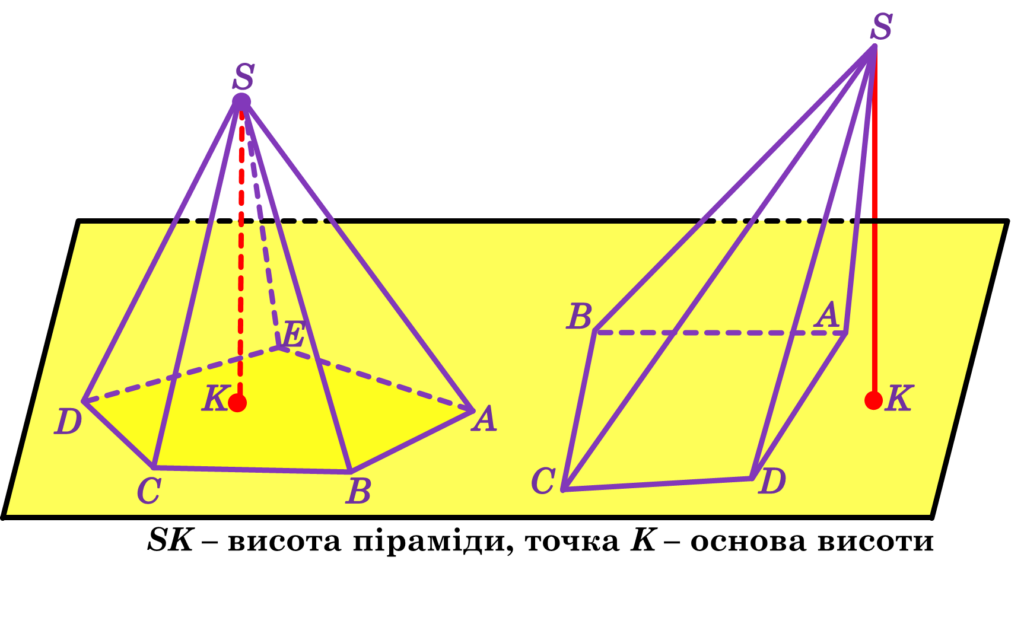
Висота піраміди – це перпендикуляр, що опущений із вершини піраміди на площину основи.
На рисунку відрізок SK – висота піраміди, точка K – основа висоти.
Правильна піраміда
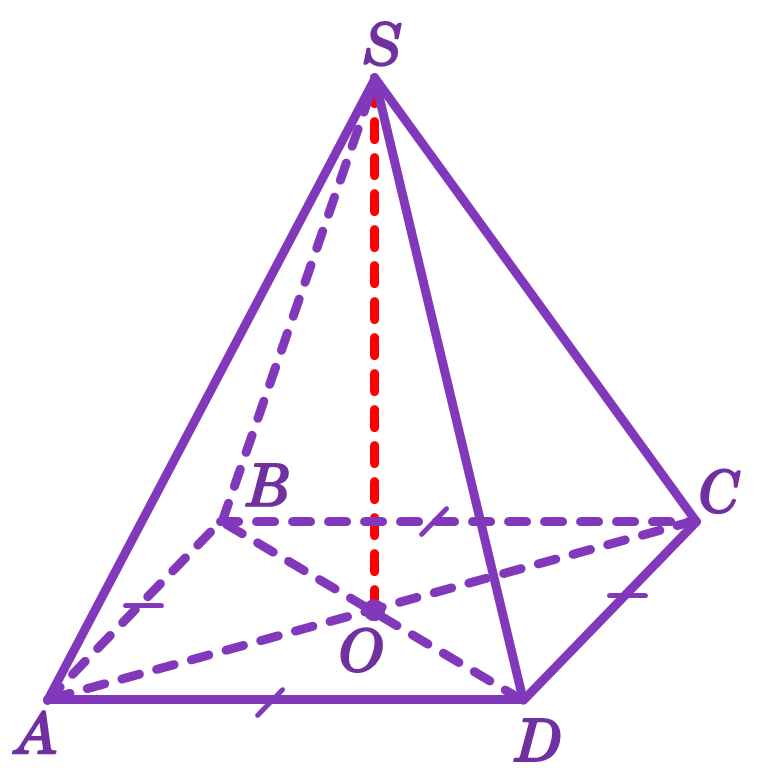
Піраміда називається правильною, якщо її основа – правильний многокутник і основа висоти піраміди є центром цього многокутника.
Побудова правильної піраміди
1.Будуємо зображення многокутника, що лежить в основі.
2.Знаходимо положення точки O – основи висоти правильної піраміди
3.Будуємо висоту піраміди
4.Сполучаємо вершину висоти з вершинами основи.
Усі бічні ребра правильної піраміди рівні.
Усі бічні грані правильної піраміди – рівні рівнобедрені трикутники.
Правильну трикутну піраміду, у якої всі грані рівні, називають правильним тетраедром.
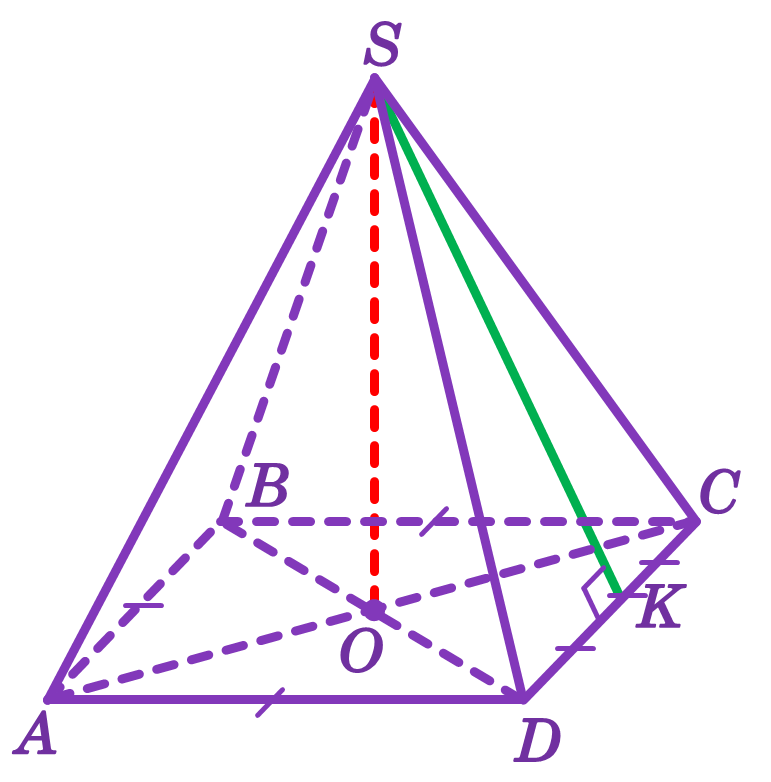
Апофемою піраміди називається висота бічної грані правильної піраміди, що проведена з вершини піраміди.
Усі апофеми правильної піраміди рівні.
SK – апофема піраміди
Діагональний переріз
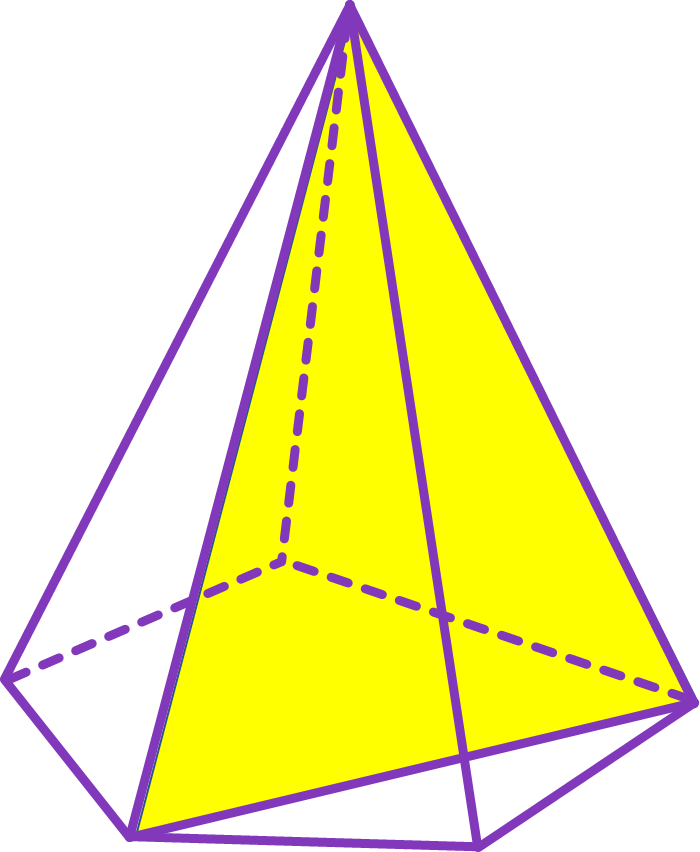
Переріз піраміди площиною, яка проходить через два бічних ребра, що не належать одній грані, перетинає площину основи піраміди по діагоналі. Такий переріз називають діагональним перерізом піраміди.
Діагональний переріз – переріз, що проходить через два несусідні бічні ребра піраміди.
Діагональний перерізом піраміди є трикутник.
Площа бічної поверхні піраміди

Площею бічної поверхні піраміди називають суму площ усіх її бічних граней.
Площа бічної поверхні правильної піраміди дорівнює половині добутку периметра її основи та апофеми.

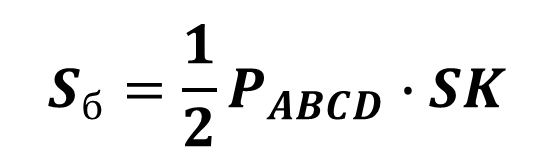
Площа повної поверхні піраміди

Площею поверхні піраміди (ще говорять: «площа повної поверхні піраміди») називають суму площ усіх її граней.

Запам’ятай!
